Synthetic Control with Goodreads and the Financial Times

11 Jan 2024

Every year, various outlets put out "Best of Year" articles for various things. In this case, the Financial Times put out Best Books of 2023, for several subjects. I was curious what the effect would be on book sales – especially because some of these books are more academic or obscure on the whole. I don't have access to book sales data, but Goodreads does have statistics on when people "add" books to their "shelves". Using this publically available Goodreads data as a proxy for interest and marketing effectiveness, we can try to estimate if the Financial Times series had a significant effect on interest in the books featured (and thus, presumably also book sales).

I made a few assumptions and caveats in this quick analysis. One assumption was that two different goodreads action statistics could be additive ("added" and "to-read"). Another was that I could try to use the other books of authors' whose books were featured in the Best Of series as a donor pool to create synthetic controls. Strong spikes for different books at different times outside of the FT Best Of publication dates I assume to be other, "exogenous" marketing/publicity efforts. Lastly, while the FT Best Of series contained many subject list Best Ofs, I scoped the analysis to Economics, History, and Politics, for ease and to restrict my web-scraping volume.

Regarding methodology, I chose synthetic control to try to estimate the effect. The gist of synthetic control is to construct a counterfactual from donor units which then allows us to peer into the un-seen, untreated outcomes of our treated units. It does this using regression to find the weights which then are applied to the donor units to properly mimic the treated unit's would-have-been future. The method is fairly recent and gaining traction in the social science literature.

There are a few reasons I chose synthetic control over other possible methods. First, marketing mix models would be one possibility but they are generally done internally where all marketing decision data is available because they are effective when one has access to the full data on marketing efforts – how "strong" those efforts were in dollar terms, when they started and stopped, etc – which we don't have. Second, after doing some reading on regression discontinuity in time, I decided it had issues that were better addressed by synthetic control. Synthetic control would better be able to deal with time-varying unobservable variables. As said in this paper: "RDiT requires assumptions for identification that are often strong and inherently untestable." While my application of synthetic control and definition of the donor pool here are imperfect, I prefer it to RDiT – and one might even argue that a simple pre-post analysis might also suffice for most situations (as they do in the aforementioned paper). But we're just having fun here, and I wanted to see what I could do with synthetic control :).

To view the dataset from above we can use panelView (authored in part by the same people who worked on gsynth, which we will introduce in a moment). As we can see we have about 40 treated books, and roughly 250 untreated as our donor pool. We can also see the (slightly) staggered treatment. We also have a significant size in terms of panel data, covering a little over five months.

At first, borrowing heavily from code in Causal Inference for the Brave and True, I created a simple synthetic control model using our treated and untreated books. I excluded about 10 books (treated and untreated) which had very high pretreatment spikes, as these reflected exogenous variation of other marketing efforts and which seemed to be heavily biasing the model (see below). Outside of these outliers, I had two main difficulties to deal with: one was that I had more than one treated unit (about 40 in my case), and the other was that I realized after a bit that the Best Of series was not all published on one day, so I actually had three different treatment periods as well.

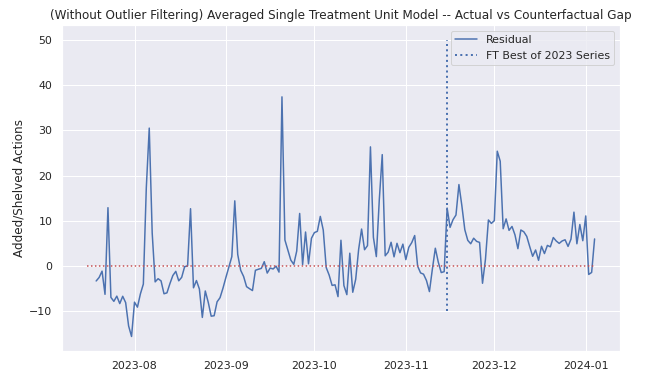
To deal with the issue of multiple treatment units I first attempted to create synthetic controls for each treated unit and add the synthetic control outcomes together. This model passed the smell test but it felt a bit crude; I wanted to see what would happen if I collapsed the treatment units into one, with an average. In the second attempt, I aggregated the treated books into a single treated unit, and this time I came up with a model that passed the smell test. However, after reading this stackexchange post, I decided to make use of the gsynth package which could help me directly address both my problems of multiple treated units and staggered treatments with a proper methodology, as opposed to my jerry-rigged solutions where I wasn't even addressing the staggered treatments (only staggered one to two days).

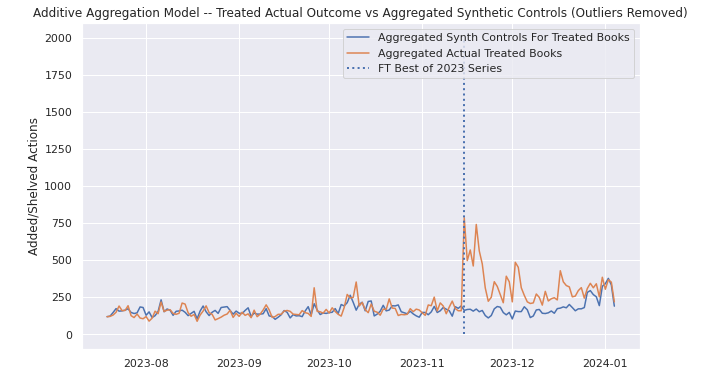
The gsynth package implements Generalized Synthetic Control, which implements a variation on synthetic control using two way fixed effects and a factor loading scheme. Importantly, it is able to incorporate multiple treated units and staggered treatments. I should note that it does have a trade off of interpretability: where synthetic control restricts weights of its constituent donors to add to 1 and be positive, generalized synthetic control is calculating factors and also does not necessarily constrain them to add to 1 and all take on positive values. As said in the paper: "estimated factors may not be directly interpretable because they are, at best, linear transformations of the true factors..."

After fitting the gysnth model, we can see that the overall results are similar to the averaged out book model I created in python which didn't properly address the multiple treatment unit or staggered treatment. However the gsynth model here performs better despite the fact that I did not exclude the outliers I mentioned above, which had severely thrown off the original model (see below).

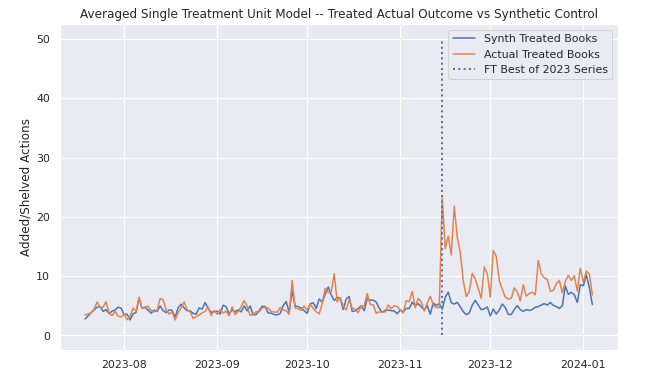
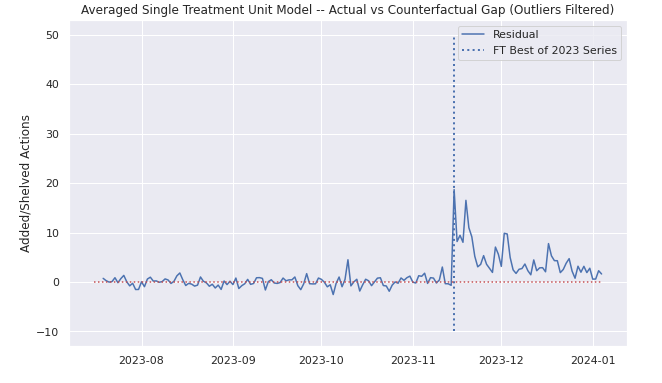
To give a singular example of the results for a single treatment unit, below are three graphs of Branko Milanovic's new book [Visions of Inequality]{.underline}, the goodreads data (with a dotted line added for treatment date), the actual versus the blue dotted synthetic control, and the gap.

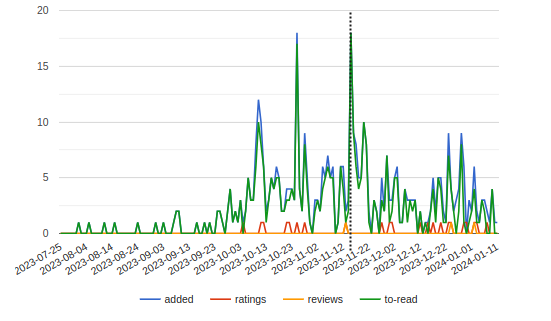
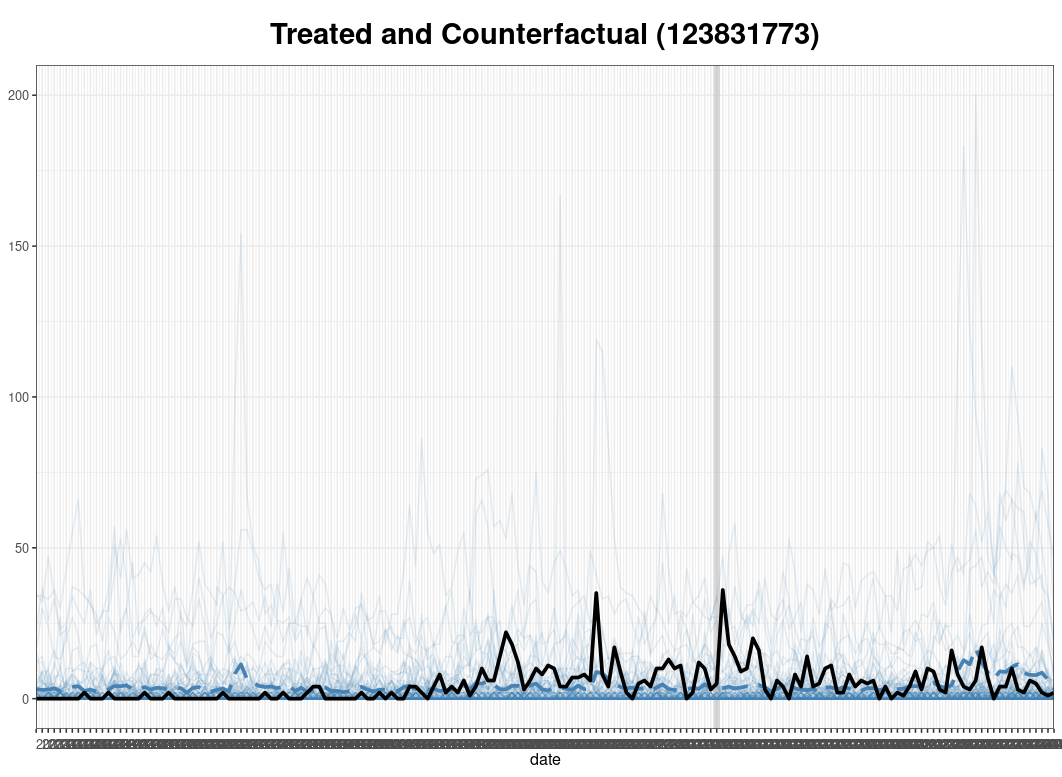
Critically we can see that the model does not overfit, but also that it does seem to be able to isolate the FT effect, even with the (perhaps janky) definition of a donor pool that we used in this analysis. Eyeballing, it seems as though the ATT really occurs over one to two weeks before trailing off into residual noise. Though perhaps a simple before-after eye test might have sufficed, I think this is a bit more fun, and it was interesting to see how synthetic control would work. You can find some of the (messy, quick – please excuse it) webscraping and modeling code here if you're interested.