Implementing Turchin's Metaethnic Frontier Theory With NetLogo

Intro

Peter Turchin is a Quantitative Biologist turned Quantitative Historian. In his approach to history he attempts to capture historical trends and patterns by leveraging data on expired agrarian societies and even adjusting his theories to attempt to encompass more modern industrial societies. Building on work by Jack Goldstone, Professor Turchin has proposed various models to explain “historical dynamics” as part of the study he calls Cliodynamics. In one of his early books on Cliodynamics, Historical Dynamics, Turchin lays out details of varous models he uses to try and understand how societies function and evolve. The Metaethnic Frontier theory is proposed to model the geopolitical dynamics of competing polities, with special attention paid to the sociological concept of Asabiya and several assumptions based on previous work. I decided it would be a fun way to try and learn more about agent-based modeling by implementing in NetLogo, a popular piece of software for Agent-Based modeling and simulation.

NetLogo

NetLogo is an environment for doing agent-based modeling and simulation. The general framework is that the “observer” manipulates “turtles” (agents), “patches” (space/territory), and “links” (relationships between turtles or patches to each other) through time (“ticks”). The GUI provides graphic representations of the model being built and run, as well as providing ways to easily plot data generated by the model, create buttons to “setup” or run (“go”) the model, and other features. The NetLogo language itself is a lisp-y agent-based language that can take some getting used to as it contains some unique concepts like “self” and “myself”. The NetLogo website also has a library of example models that are often helpful for understanding how to implement certain concepts.

The Theory

Asabiya is a concept from the writings of Ibn Khaldun which Turchin defines as “the capacity for collective action” of a society. The Metaethnic Frontier theory is meant to incorporate asabiya as a key factor in predicting the dynamics of imperial agrarian societies - how they grow, shrink, and begin. Turchin posits that multi-level selection can help us identify the dynamics of asabiya in groups. He follows by noting three ways in which the logic of multi-level selection can be relevant in understanding change in “collective solidarity”: intergroup conflict, population and resource constraints, and ethnic boundaries.

For small groups, intergroup conflict can increase asabiya as people need to band together to survive as a group. Conversely (again for small groups), a large population with respect to available resources can decrease asabiya as individuals compete for limited resources. For larger groups, Turchin proposes that ethnic boundries can influence how bands of small groups with moderate ethnic differences can band together against people who are even more “ethnically distanced” - more “Other”. In this process of small groups banding together against peoples more Other than themselves, they can form what Turchin calls a Metaethnic Frontier, which manifests in a more symbolic form (eg: exclusionary religion). Turchin notes that the this ethnic boundry dynamic which generates asabiya in a large group (composed of smaller groups) is weak because as the size of the group grows larger, the central regions are less exposed to intergroup conflict and asabiya decreases, leading to greater internal division. Finally, Turchin notes that all three aforementioned possiblities occur at regions which constitute imperial and metaethnic frontiers (imperial and metaethnic frontiers often coincide, he notes). Its is in these regions of intense dynamics where asabiya is forged which are most prone to ethnogenesis - where new ethnic identites are formed, and new empires are seeded.

The Model

The model is predicated on a straightforward set of equations that dictate how values change over the discrete time of the model. We presume a matrix of cells (“patches”) where each cell is essentially a regional polity - either as part of the “non-imperial hinterland” or as a piece of an empire. Each cell (regional polity) takes on a regional asabiya, and an imperial asabiya (for hinterland regions I set these two variables to be the same value). In addition, each cell is assigned an imperial index (0 for hinterland, and some integer for a cell belonging to an empire). I also gave a unique color for each imperial index. Likewise, cells are also assigned some other variables used for calculations, such as the imperial “center of gravity”, average imperial asabiya, and number of regions constituting each empire.

The regional (cell) asabiya value over time steps (“ticks” in NetLogo) are determined as follows. If the region has a neighbor (not including diagonally adjacent cells) which is of a different imperial index, then asabiya increases in accordance with the following formula:

Here, r_0 signifies some defined parameter. Indices x, y, and t represent x and y coordinates of the cell in the matrix and the time t in ticks, respectively. In the other case, if the region in question is neighbors only with cells of the same imperial index, asabiya decreases according to the following formula:

Here, delta signifies some defined parameter/constant. These parameters are set as global variables in the model.

Note: I may have differed from the model defined in the book in this respect. I allowed for hinterland regions to attack other 0-indexed regions and possibly conquer them. In addition, I randomly assigned their initial regional/imperial asabiya value as opposed to setting them all equal to 0. This is something I might tweak in a second pass.

Calculating the imperial asabiya at each time step, we simply take the average of the region asabiya of all cells with the respective imperial index:

Here, A signifies number of regions an empire i controls at time step, t. We will now use the imperial asabiya to help calculate a definition of a region’s power, which indicates how well it can attack or defend itself. Cells attack by randomly choosing a neighboring cell with a differing imperial index. Below is the region/cell’s power definition needed for calculating outcomes when cells decide to attack each other:

d here represents the distance between the cell in question and the average of the x and y coordinates of the empire’s cells. This average location is the “center of gravity” of the empire. h signifies how well imperial power travels over distance. The significance here is that as distance between the imperial center of gravity and the regional cell grows larger, it mitigates the power the cell. Likewise, modulating h affects how much distance plays a role in the polity power calculation. Next, a cell wins an attack and takes over the defending cell (change of imperial index) when the following is true:

Delta_p denotes a parameter for power differential necessary to declare an attack successful.

Finally, at the end of a time step, we calculate whether an empire collapses due to falling below a critical imperial asabiya threshold. If this occurs, the empire’s cells are changed to be non-imperial hinterland.

The Implementation

After implementing this in NetLogo, I saw many of the dynamics Turchin noted, as well as instances where my implementation might have deviated in important ways. One important difference I should note is the beginning. I do as Turchin specifies in starting out with a set of four neighboring polities which comprise of the first empire, but in many cases, it is immediately destroyed as in my implementation. As I noted above, I believe this is because I am currently not initializing all hinterland region with 0 asabiyah from the beginning but randomizing their asabiyah such that they will in fact immediately begin to conquer each other. As a result you can see an initial cambrian explosion of small empires and a subsequent consolidation stage where a handful of empires make it out of the initial chaos alive.

To begin with, each NetLogo model requires two procedures: a setup procedure and a go procedure, which initialize and execute the model. Below is the code for the go procedure.

;Algorithm for time steps
to go
  let empires (remove-duplicates [imperialindex] of turtles)

  update-asabiya

  ask turtles [
    calculate-imperial-asabiya
    calculate-imperial-num-regions-controlled
    calculate-imperial-center
    calculate-turtle-power
  ]

  ;attacks
  decide-attack

  ;at end of each time period, check for imperial collapse
  calc-imperial-collapse

  tick
end

In this go procedure we see that we can execute procedures such as update-asabiya as well as other commands. The ask turtles command here is a function ask which takes two arguments: a) an agent or agentset (turtles) and b) a list of commands. let here is allowing us to define a local variable that will be recalculated each timestep and is used in another computation in this go procedure. tick is updating the model to start the next discrete time block.

Notice that I don’t do all of the procedures in one ask turtles command. The ask turtles command works by going through the agentset - turtles (a cell/polity) in this case - and running all commands in the command list, one by one - not concurrently. With update-asabiya, for example, I want to calculate regional asabiya for all turtles before any turtle does any other actions or calculations in the timestep because some of them use the updated regional asabiya. Therefore I isolate that computation in its own ask turtles block and procedure, seen here:

to update-asabiya
ask turtles [
  ifelse any? ( turtles-on neighbors4 ) with [ imperialindex = 0 or imperialindex != [imperialindex] of myself ]
  ;let tminusoneasabiya asabiya
  ; Sx,y,t+1 = Sx,y,t + r0Sx,y,t(1-Sx,y,t)
  [ set asabiya (asabiya + r-o * asabiya * (1 - asabiya) ) ]
  ; Sx,y,t+1 = Sx,y,t - dSx,y,t
  [ set asabiya (asabiya - delta * asabiya ) ]
  ]
end

Much of the NetLogo code looks more or less like the above - procedures defining computations against certain agentsets, moving forward in time, setting variables, etc. Now, if we run the model, we can see the initial growth and then consolidation of polities (which is likely not how Turchin’s model in the beginning stages would look, if followed to the tee.

Once there is a more conslidated set of polities - while still having significant evolution - we can see a great example of a new state appearing at the intersection of some frontiers and expanding. On the right, the light purple empire emerges out of the frontier region between two other large empires. Ethnogenesis in action.

Finally, we can witness some empire collpase when a few empires’ collective imperial asabiya falls below the critical point.

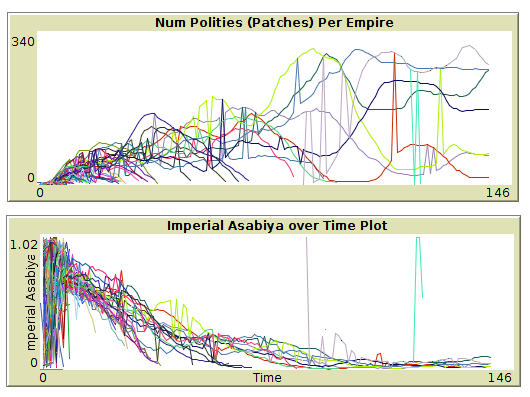
I also made some graphs showing polity size and imperial asabiya over time. As expected, as time goes on and the surviving empires become larger regions, the imperial asabiya descreases due to the low asabiya of the central regions of said empires. Likewise, we can see the average size of the polities increase over time in this first cycle, at least.

To generate gifs from the NetLogo model run, I used the export-view function in conjunction with this imagemagick snippet which sorts the images by filename when creating the gif

Thoughts

NetLogo was an interesting experience, but I’m sure I haven’t mastered it yet. As this was my first attempt at using NetLogo, I found myself at a bit of a loss at how to implement this particular model and concepts like “self” vs “myself” were quite foreign. I was able to get by without needing to use “links” so I still know very little about them. The basic thrust of the logic of my implementation in NetLogo was to make each patch host exactly one turtle, where I then just dealt with turtles instead of patches. Now looking back, I suspect you should be able to do with just with patches, avoiding the extra complexity. I may revisit that in the future. In general I was a bit unsure of how idiomatic my code was for this, and I felt that I had hacked together some parts in unelegant ways (eg: chosing a non-used unique color for a new empire). I’m actually not sure whether my implementation is entirely faithful to the original model, as a few details were not entirely clear - and I may have also made some mistakes on this first pass. Nonetheless, I was able to see some of the same dynamics that Turchin describes in the book and the general thrust still seemed to hold quite well. You can see the NetLogo model code here. If you have any feedback, questions, or comments about the code or otherwise, do reach out.

If you’re still curious, another explanation/implementation of the Metaethnic Frontier theory (in unity) can be found in this blog post.